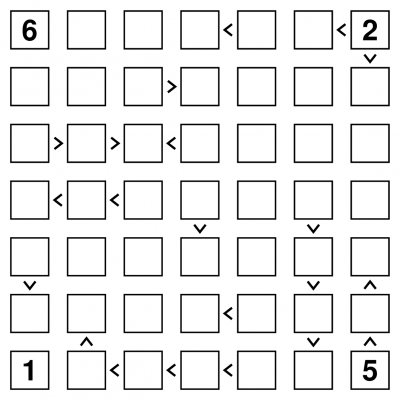
A standard Futoshiki puzzle consists of a grid of squares, separated by either spaces or inequality signs: greater-than signs (>) and less-than signs (<).
The aim is simple: place the digits 1 to 7 (or whatever the puzzle size is) into the puzzle grid so that each digit occurs once in every row and column, whilst also obeying the inequality signs.
Some digits may already be given - these, along with the inequality signs, constrain the puzzle in such a way that there is only one possible solution, which can always be reached via reasonable logical deduction. Guessing is never required.
We can supply Futoshiki puzzles in a wide range of sizes, and optionally with some additional variations such as Futoshiki-X (with diagonal regions). We can also supply Inequality Sudoku, which is essentially a Futoshiki with additional box regions, as in regular Sudoku.
All of our puzzles are either entirely hand-made or have significant manual input into the process.